Gruppen – Csoportok – Groups

Unter einer Gruppe verstehen wir bekanntermaßen eine Menge $G$ mit einer zweistelligen Operation $\circ$ auf derselben mit folgenden Eigenschaften.

Assoziativität:
$\forall\,a, b, c \in G \,:\, (a \circ b) \circ c \,=\, a \circ (b \circ c)$
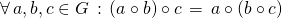
Linkes und rechtes Einselement:
$\exists\,e_l \in G \, \forall\, g \in G \,:\, e_l \circ g \,=\, g$
$\exists\,e_r \in G \, \forall\, g \in G \,:\, g \circ e_r \,=\, g$
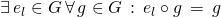
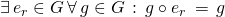
Daraus folgt unmittelbar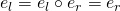 $e_l = e_l \circ e_r = e_r$ , d.h. es linkes und rechtes Einselement sind identisch : $e_l = e_r = e$ .
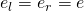Linkes und rechtes Inverses:
$\forall\,g \in G \exists\,g_l^{-1} \,:\, g_l^{-1} \circ g \,=\, e$
$\forall\,g \in G \exists\,g_r^{-1} \,:\, g \circ g_r^{-1} \,=\, e$
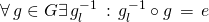
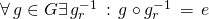
Daraus folgt:
$g_l^{-1} \,=\, g_l^{-1} \circ e \,=\, g_l^{-1} \circ \left( g \circ g_r^{-1} \right) \,=\, \left( g_l^{-1} \circ g \right) \circ g_r^{-1} \,=\, e \circ g_r{-1} \,=\, g_r^{-1}$
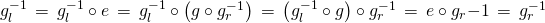
Also sind linkes und rechtes Inverses identisch und wir schreiben dafür einfach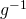 $g^{-1}$ .
Kommutativität:
Gilt außerdem noch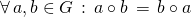 $\forall\, a, b \in G \,:\, a \circ b \,=\, b \circ a$ , dann heißt die Gruppe kommutativ oder Abelsch (nach dem norwegischen Mathematiker Niels Henrik Abel, 1802 — 1829)

Sind $A$ und $B$ Teilmengen und $g$ ein Element von $G$ , dann können wir $A \circ B$ , $A \circ g$ und $g \circ B$ definieren:
$A \circ B \,:=\, \left\{ a \circ b \left| a \in A \wedge b \in B \right. \right\}$ sowie
$A \circ g \,:=\, A \circ \left\{ g \right\}$ und $g \circ B \,:=\, \left\{ g \right\} \circ B$ .

Eine Menge $H \subset G$ ist eine Untergruppe von $G$ , wenn die Gruppenoperation $\circ$ und die Inversenbildung nicht aus $H$ herausführen: $\forall\, a, b \in H \,:\, a \circ b \in H$ und $\forall\, h \in H \,:\, h^{-1} \in H$ . Wir schreiben dann $H \leq G$ bzw. – wenn $H$ eine echte Teilmenge von $G$ ist: $H < G$ .

Ist $G$ eine Gruppe und $H \leq G$ eine Untergruppe von $G$ , dann bezeichnen wir die Mengen $g \circ H$ bzw. $H \circ g$ als die linken bzw. rechten Nebenklassen von $H$ . Man sieht leicht, dass für zwei Elemente $g_1, g_2 \in G$ die Abbildung $g_1 \circ H \ni x \longmapsto g_2 \circ g_1^{-1} \circ x \in g_2 \circ H$ wohldefiniert und bijektiv ist. Außerdem gilt immer entweder $g_1 \circ H \,=\, g_2 \circ H$ und $g_2 \circ g_1^{-1} \in H$ oder aber $g_1 \circ H \cap g_2 \circ H \,=\, \emptyset$ und $g_2 \circ g_1^{-1} \not\in H$ . Damit bilden die linken Nebenklassen eine Äquivalenzrelation mit gleichmächtigen Klassen. Das gleiche gilt natürlich für die rechten Nebenklassen.
Darüber hinaus ist die Abbildung $g_1 \circ H \ni x \longmapsto g_1^{-1} \circ x \circ g_2 \in H \circ g_2$ ebenfalls eine wohldefinierte, bijektive Abbildung. Das bedeutet, dass zum einen die Mächtigkeit einer beliebigen linken Nebenklasse mit der einer beliebigen rechten Nebenklasse übereinstimmt und zum anderen die Anzahl der linken mit der Anzahl der rechten Nebenklassen (jeweils als Mächtigkeit zu verstehen) übereinstimmt.

Ist $A \subseteq G$ eine Untermenge von $G$ , dann generiert sie eine Untergruppe von $G$ – dies ist der Schnitt aller Untergruppen von $G$ , die $A$ enthalten:

$G \geq \left[ A \right] \ = \ \bigcap\limits_{H \leq G \wedge A \subseteq H} H \ .$

Besteht $A$ nur aus dem Element $a \in G$ , dann ist die Menge $\left\{ \ldots, a^{-2}, a^{-1}, e, a, a^2, a^3, \ldots \right\} \ = \ \left[ a \right]$ die von $a$ generierte Untergruppe von $G$ . Ist diese wiederum endlich, dann heißt das Element $g$ zyklisch und die Ordnung von $a$ bezeichnet die Anzahl der Elemente der von $a$ generierten Untergruppe: $o(a) = \operatorname{ord}(a) \,=\, \left| \left[ a \right] \right|$ .
Die Ordnung eines zyklischen Elements $a \in G$ ist die kleinste natürliche Zahl $n > 0$ , für die gilt $a^n = e$ . Gleichzeitig gilt für beliebige natürliche oder ganze Zahlen $n \in \mathbb{Z}$ : $a^n = e \Longrightarrow \operatorname{ord}(a) | n$ .

Eine Untergruppe $N \leq G$ heißt Normalteiler von G, wenn gilt: $\forall\, g \in G \,:\, g \circ N \,=\, N \circ g$ . Wir schreiben dann $N \trianglelefteq G$ bzw. – wenn $N$ eine echte Teilmenge von $G$ ist: $N \triangleleft G$ . Damit sind die linken und rechten Nebenklassen für gleiche Elemente von $G$ identisch und wir müssen nicht zwischen linken und rechten Nebenklassen unterscheiden.

Man kann recht leicht zeigen, dass für einen Normalteiler $N \trianglelefteq G$ die Abbildung $G \ni x \longmapsto x \circ N$ auf der Menge der (linken oder rechten) Nebenklassen eine wohldefinierte binäre Operation erklärt:

$\left( g_1 \circ N \right) \circ \left( g_2 \circ N \right) \longmapsto \left( g_1 \circ g_2 \right) \circ N$

und auch die Abbildung

$\left( g \circ N \right)^{-1} \longmapsto g^{-1} \circ N$

ist wohldefiniert. Des weiteren bilden die Mengen der (linken oder rechten) Nebenklassen mit diesen Operationen eine Gruppe. Diese heißt die Faktorgruppe von $G$ bezgüglich $N$ und wir schreiben $G / N$ . Die Abbildung $g \longmapsto g \circ N$ ist ein Homomorphismus, dessen Kern gerade $N$ ist.

Umgekehrt ist für einen Gruppen-Homomorphismus $\varphi : G \longrightarrow G'$ dessen Kern $N := \operatorname{ker}\varphi \,:=\, \left\{ g \in G \left| \varphi(g)=e \right.\right\}$ ein Normalteiler von $G$ und die Faktorgruppe $G / N$ ist isomorph zum Bild von $\varphi$ :

$G / \operatorname{ker}\varphi \ \cong\ \operatorname{im} \varphi \ .$

Dies ist der erste Homomorphiesatz der Gruppentheorie.

Für einen Normalteiler $N \trianglelefteq G$ und den zugehörigen Homomorphimus $\varphi : G \longrightarrow G / N$ ist der Kern von $\varphi$ gerade $N$ und umgekehrt ist für einen Homomorphismus $\varphi:G \longrightarrow G'$ der kanonische Homomorphimus $G \longrightarrow G / \operatorname{ker}\varphi$ identisch mit $\varphi$ , wenn man von Isomorphien absieht.

Schreibe einen Kommentar Antworten abbrechen