From Wikipedia we have for a ring ![]() and a group
and a group ![]() a new ring written as
a new ring written as ![]() that is defined on the functions
that is defined on the functions ![]() with finite support and addition and multiplication defined as follows.
with finite support and addition and multiplication defined as follows.
![]()
and
![Rendered by QuickLaTeX.com \[\sum\limits_{g \in \mathcal{G}} \phi_g g \ \cdot \ \sum\limits_{g \in \mathcal{G}} \psi_g g \ := \ \sum\limits_{g \in \mathcal{G}} \left( \sum\limits_{u,v \in \mathcal{G} | uv = g} \phi_u \cdot \psi_v \right) g \ = \ \sum\limits_{g \in \mathcal{G}} \left( \sum\limits_{h \in \mathcal{G}} \phi_{h} \cdot \psi_{h^{-1}g} \right) g\]](http://mathematics.steffenzopf.de/wp-content/ql-cache/quicklatex.com-81fb299aa26cbde83a45014c7c015081_l3.png)
Here, ![]() stands for a (formal) sum of elements of
stands for a (formal) sum of elements of ![]() with coefficients taken from the ring
with coefficients taken from the ring ![]() . This makes sense as long as the functions in question have finite support, i.e.
. This makes sense as long as the functions in question have finite support, i.e. ![]() .
.
The group ring is written ![]() . It is clear that the group ring is also a module over the ring
. It is clear that the group ring is also a module over the ring ![]() . For an element
. For an element ![]() let us define the following mapping (action) on the group ring
let us define the following mapping (action) on the group ring
![]()
This is nothing else but a representation of the group ![]() on the linear mappings of the group ring as a module.
on the linear mappings of the group ring as a module.
If ![]() is a field the group ring is called a group algebra over the field. In this case the group action from above is nothing else but a representation of the group on the linear mappings of the group algebra as a vector space.
is a field the group ring is called a group algebra over the field. In this case the group action from above is nothing else but a representation of the group on the linear mappings of the group algebra as a vector space.
As an example let us investigate the (multiplicative) group of the ![]() -th unit roots,
-th unit roots, ![]() . Then we have for an arbitrary ring
. Then we have for an arbitrary ring ![]() an element of
an element of ![]() :
:
![]()
with
![]()
For a product of 2 elements we get
(1) 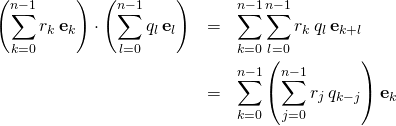
taking ![]() and analogously for
and analogously for ![]() . The coefficients of the product are the result of a convolution of the two
. The coefficients of the product are the result of a convolution of the two ![]() -element series
-element series ![]() and
and ![]() .
.