Facebook-os Feladat I – Steffen Zopf

Melyik nagyobb az 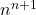$n^{n+1}$ vagy az 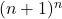$(n+1)^n$ , ahol az n tart a végtelenhez.

Maga a feladat nem nagyon értelmes, hiszen nem világos, hogy mit jelent az a kifejezés „ahol n tart a végtelenhez“ ebben az összefüggésben. Viszont meg lehet vizsgálni a két sorozat egymáshozvaló viszonyát.

Legyen tehát

$a_n := n^{n+1} \quad \text{és} \quad b_n := (n+1)^{n}$

Vegyük a tagok 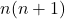$n(n+1)$ -edik gyökét — ezzel nem változtatjuk meg a két sorozat viszonyát.

$A_n := n^{\frac{1}{n}} \quad \text{és} \quad B_n := (n+1)^{\frac{1}{n+1}}$

Itt pedig 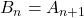$B_{n} = A_{n+1}$ ugyanaz a sorozat.

Ha most az 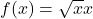$f(x) = \sqrt{x}{x}$ függvényt tekintjük, akkor ennek logaritmusának a deriváltja

$\frac{d}{dx} \log{f(x)} \ = \ \frac{d}{dx} \left( \frac{1}{x} \log{x} \right) \ = \ \frac{1 - \log{x}}{x^2}$

Ez pedig negatív illetve pozitív a szerint, hogy 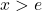$x > e$ illetve 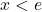$x < e$ . Következéképpen az 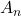$A_n$ sorozat 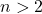$n > 2$ -re szigorúan monoton csökkenő.

Schreibe einen Kommentar Antwort abbrechen